Importance of Eccentric Wind Loading on Monopitch Module Mounting Structures
Jay Jain
Jay.Jain@sgurrenergy.com
Niraj Mehta
Niraj.Mehta@sgurrenergy.com
Download as PDF
Abstract
Wind load governs the design of the mounting structures of solar panels which constitute approximately 10 to 15 percent of the total project cost. Wind load design of the ground-mounted photovoltaic (PV) power plants requires interpretation of the design code considering the particularities of these structures. Structural failures of utility scale PV plants are rare events, but some failures have still been observed in code-compliant structures.
Wind loads are calculated using the static pressure coefficients provided in national as well as
international design standards. In the Indian Solar industry, the wind loads are applied uniformly
over the entire panel, acting as monoslope canopy, based on older version of IS875: Part 3. This paper demonstrates that this is not a precise method of wind load application and; provides a detailed description of eccentrically distributed wind load application based on IS 875: Part 3 (2015) and various other international design codes.
INTRODUCTION
Over last decade, solar PV industry has endured remarkable advancement in terms of both efficiency and cost reduction. PV module is the key component of a solar PV plant, however it should be noted that the module mounting structure plays an equally critical role in reliability and durability of solar PV plants that have designed life of more than 25 years.
The falling tariff trend has posed pressure on balance of system (BoS) cost and module mounting
structure is most sought after plant equipment which are being compromised in order to cut down
the cost of the project. This is usually done by reducing the section sizes of the supporting module
mounting structure.
The prospect of reducing the overall project cost is good, however as per SgurrEnergy’s experience the focus has been on reducing the weight of the structure while the strength of the structure to sustain the gust of wind are being compromised. Focusing on the evidences from India, there have been numerous incidences of MMS failures at lower wind speed.
Structural failures have been observed in code-compliant ground-mounted systems during wind events at wind speeds significantly less than design wind speed. The current industrial research has been focused on determining the cause of failure in otherwise code-compliant structures and improving correct method of application of wind loads.

Figure 2-1: Failure of the complete Module Mounting table under wind loading
Source: www.rmi.org

Figure 2-2: Failure of the part of Module Mounting Structure under wind loading
Source: pv-magazine-usa.com
Application of wind load governs the design of the module mounting structure. Due to lack of solar specific design code, most designers typically follow the design procedures recommended by building codes meant for large sloped roofs. This may lead to inappropriate and inaccurate results leading to unsafe designs. Though, the current wind design standards have a very wide scale of applications, they do not cover solar specific wind design guidelines.
Through this paper SgurrEnergy intends to presents the precise and specific method of application of wind loading on the mounting structure with reference to explicit notes provided in the Indian design standards and international standards.
Eccentric Wind Loading – A Technical Investigation
Several designs elements are required to be considered during MMS design. Application of wind load is one such important element which is generally compromised. The current industry trend of MMS design is to assume wind pressure acting uniformly over the entire solar panel, such that the force acts at the centre of the distributed area as shown in the figure below.
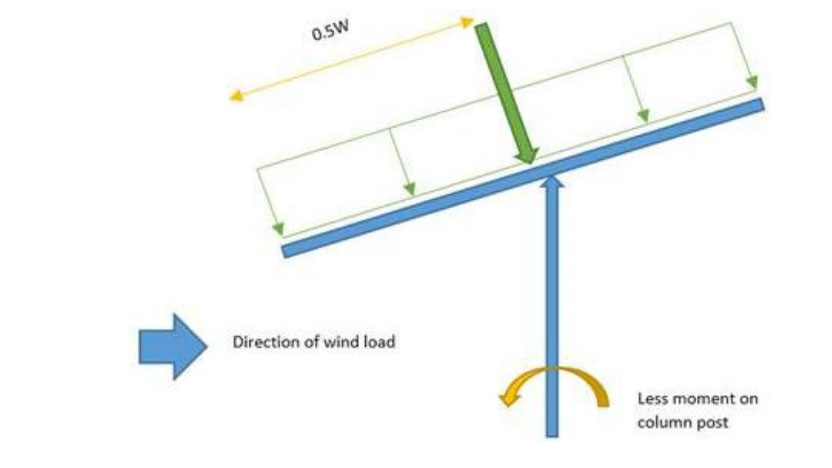
Figure 3-1: Uniform Wind load distribution
Here, w= Length of entire assembly/ canopy.
SgurrEnergy would like to call/draw attention to the note provided below the Table 8 of IS 875
(Part 3): 2015 states that the wind load shall be applied in such a way that the centre of pressure shall act at 0.3w from windward edge and not at the centre of entire assembly (0.5w). Furthermore, Table 8 of IS 875 (Part 3): 2015 provides the pressure coefficients for mono-slope free roofs. As illustrated in figure below, code also provides the method of application of load.
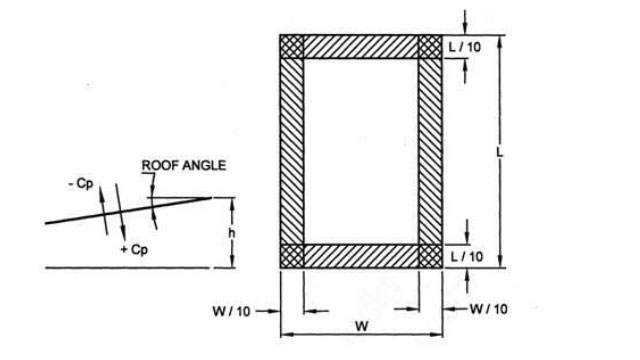
NOTES
1 For Monopitch canopies the center of pressure should be taken to act at 0.3 w from the windward edge.
2 W amd L are overall width and length including overhangs.
The note number 1 implies that the load application on mono-pitch canopies shall not be uniformly
distributed load. The pressure/load shall act eccentrically on surface. Figure below illustrates the load application in accordance with the code requirements.

Figure 3-2: Eccentric Wind load distribution
Methodology and Sample Study
In this part of the paper, SgurrEnergy intends to explicate the procedure to calculate forces on purlins of the module mounting structures for uniform and eccentric wind loading through a case study.
Case Study: The description of the MMS under consideration is as follows,
The Table configuration is 2Px30 and the fixed tilt is 20°. The Module size 2108mm x 1048mm x 40mm having weight 24.9kg separated by distance of 20mm. The structure lies in the region of basic wind speed 47m/s.
As per IS 875 (3): 2015,
- Design wind speed Vz = K1 K2 K3 K4 Vb
- Basic wind speed Vb = 47m/s
- Risk coefficient K1 = 0.9
- Terrain, height and structure size factor K2 = 1.0
- Topography factor K3 = 1.0
- Importance factor K4 = 1.0
- Hence, Vz = 42.30m/s
- Basic Wind Pressure Pd = 0.6 Vz2
- Pd = 1.074KN/m2
- Design Wind pressure Pz = Kd Ka Kc Pd
- Wind directionality factor Kd = 0.9
- Area averaging factor Ka = 1.0
- Combination factor Kc = 1.0
- Hence, Pz = 0.966KN/m2
- Now, as per Table no.7 IS 875(3): 2015, for tilt angle of 20°,
- Downward Wind Coefficient Cpd = 0.80
- Upward Wind Coefficient Cpu = -1.30
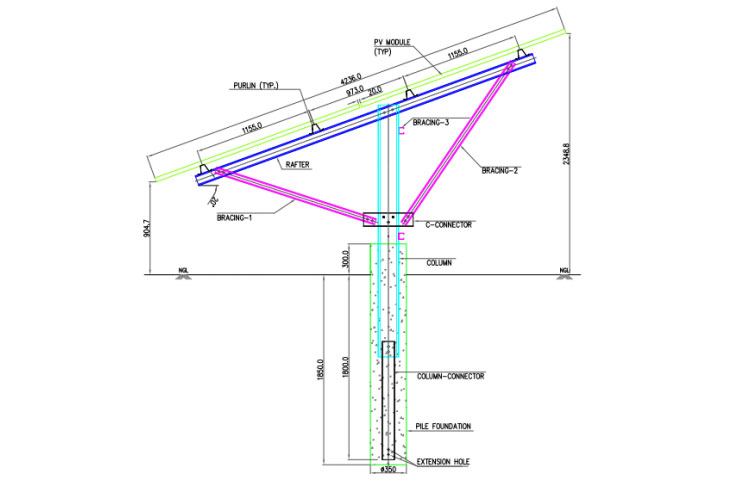
Figure 4-1: Sectional View of MMS under consideration
Old Method: - Uniform Wind Loading
CASE 1: - Downward Wind force
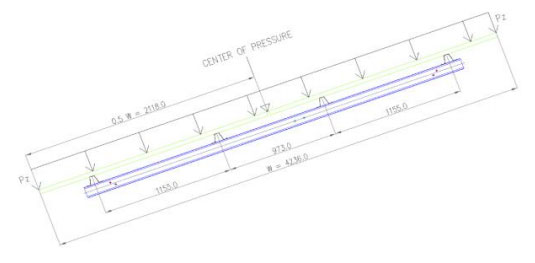
In this case, the pressure is distributed uniformly over the panels as shown in the figure above. The centre of pressure lies exactly at the Centre of the two panels as shown
Total Force (per unit width),
Ftotal = Cpd x A x Pz
Ftotal = 0.80 x (4.236 x 1) x 0.966
Ftotal = 3.273 KN per unit width
Updated Method: - Eccentric Wind Loading
CASE 1: - Downward Wind force
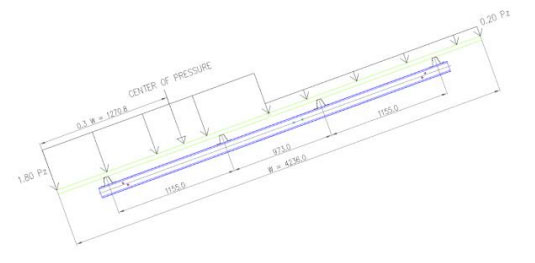
In this case, the pressure is distributed uniformly in two parts having intensities 1.8Pz and 0.2Pz as shown in the figure to assure that the Centre of pressure is acting at 0.3W.
C.G Calculation: -
Distance of CP = P1 x X1 + P2 x X2 / (P1 + P2) = (1.8 Pz x 1059 + 0.2 Pz x 3177) / 2.0Pz = 1270.8
And, 1270.8/4236 = 0.3
Thus the Centre of Pressure acts at 0.3W
Total Force (per unit width),
Ftotal = F1total + F2total
Ftotal = 0.80 x (2.118 x 1) x 1.8 x 0.966 + 0.80 x (2.118 x 1) x 0.2 x 0.966
Ftotal = 2.946 + 0.327
Ftotal = 3.273 KN per unit width
Thus, the total force coming on the entire assembly shall be same in both the cases; only the distribution of this force on the purlins will be different, which is presented in the below section.
Load distribution on Purlins: - The total force as calculated above is equally distributed on all the four purlins as shown in the figure below
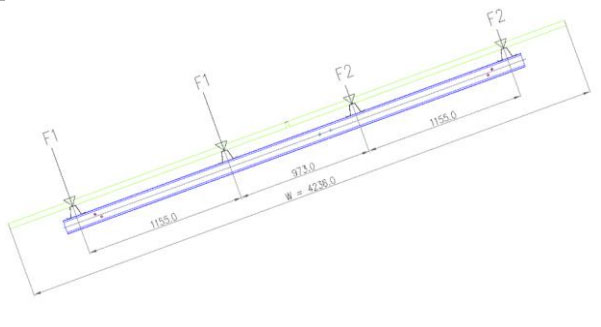
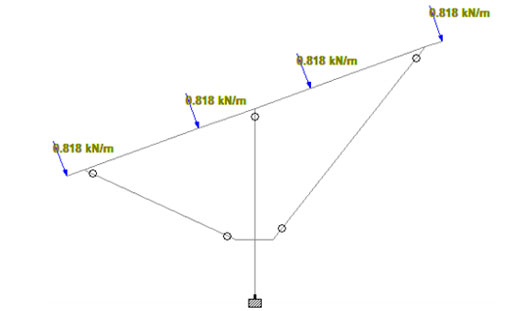
- F = 3.273 / 4
- F = 0.818 KN/m
Load distribution on Purlins: - The force distribution on the purlins is as per the pressure distribution on the respective panels. The purlins lying in the high pressure region will have higher forces and vice versa.

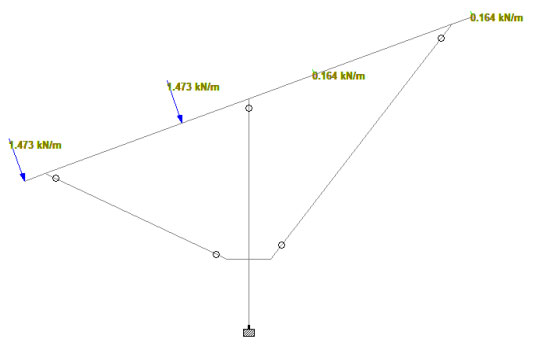
- F1 = F1total / 2 = 2.946 / 2
- F1 = 1.473 KN/m
- F2 = F2total / 2 = 0.327 / 2
- F2 = 0.164 KN/m
CASE 2: - Upward Wind force
The upward wind forces will be calculated in similar fashion by using upward wind pressure coefficients.
Total Force (per unit width),
- Ftotal = Cpu x A x Pz
- Ftotal = -1.3 x (4.236 x 1) x 0.966
- Ftotal = 5.320 KN per unit width
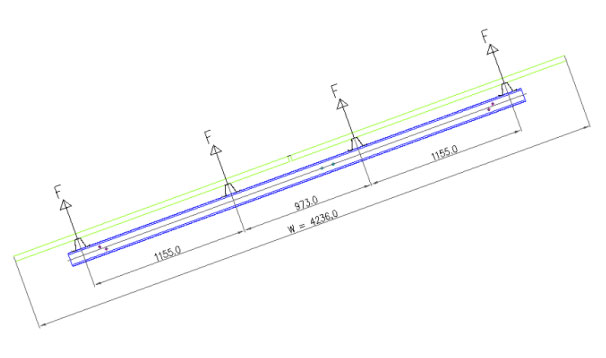
- F = 5.320 / 4
- F = 1.330 KN/m
CASE 2: - Upward Wind force
The upward wind forces will be calculated in similar fashion by using upward wind pressure coefficients.
Total Force (per unit width),
- Ftotal = F1total + F2total
- Ftotal = 1.3 x (2.118 x 1) x 0.2 x 0.966 + 1.3 x (2.118 x 1) x 1.8 x 0.966
- Ftotal = 0.532 + 4.787
- Ftotal = 5.320 KN per unit width
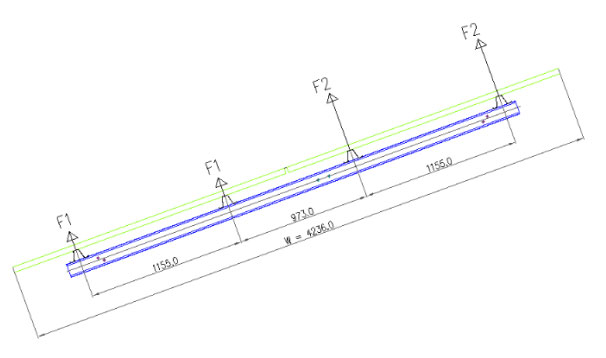
- F1 = F1total / 2 = 0.532 / 2
- F1 = 0.266 KN/m
- F2 = F2total / 2 = 4.787 / 2
- F2 = 2.393 KN/m
ANALYTICAL STUDY
In this study, static analysis of the Module mounting structure is carried out in Staad Pro for uniform as well as
eccentric loading calculated in the above sections. The sectional view of the Staad model is provided below:
Uniform loading applied on purlins:
Wind Upward Case: -
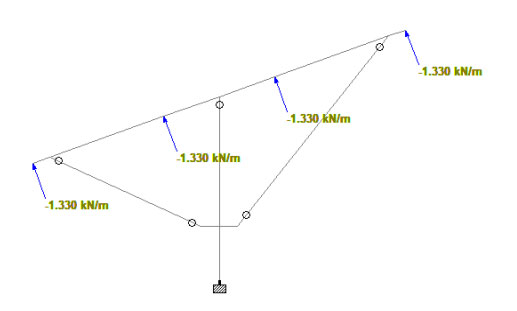
Wind Upward Case: -
Eccentric loading applied on purlins:
Wind Upward Case: -
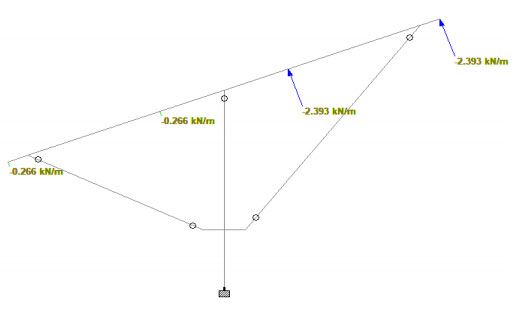
Wind Upward Case: -
Check for Deflection:
Deflections of the structural elements of the MMS based on the worst load combination shall be limited to an acceptable level. The deflections obtained are provided below:
| Member |
Section size |
Span (mm) |
Deflection Criteria |
Allowable Deflection (mm) |
Uniform Loading (mm) |
Eccentric Loading (mm) |
Remarks |
| Column Post |
150CS50x3.15 |
1242 |
L/150 |
8.28 |
6.71 |
19.60 |
Deflection exceeds the permissible limits in Eccentric Loading |
| Rafter Cantilever Top |
70CS50x1.5x10 |
1642 |
L/150 |
10.94 |
7.24 |
27.82 |
| Rafter Cantilever Bottom |
70CS50x1.5x10 |
1642 |
L/150 |
10.94 |
8.85 |
28.79 |
| Central Purlin |
90HU40x25x0.8 |
3150 |
L/180 |
17.50 |
5.53 |
10.72 |
Safe |
| End Purlin |
90HU40x25x0.8 |
3150 |
L/180 |
17.50 |
4.88 |
10.84 |
Safe |
| Purlin Cantilever |
90HU40x25x0.8 |
1000 |
L/180 |
5.55 |
0.07 |
4.22 |
Safe |
The deflections for the MMS members are within the permissible limits for uniform loading. However, the
deflections in column post and rafters exceed the permissible limit for eccentric wind loading. The deflections
observed for eccentric loading almost three times of that observed for uniform loading.
Check for Forces:
A major increase is observed in the Bending moment of the columns due to application of eccentric wind loading
which can be verified from the below provided figures:
In case of eccentric loading, the wind forces act predominantly on the half part of the canopy as seen in the above load calculations. Hence, a tremendous increase is observed in the moments generated in the columns. The moment due to lateral wind forces under eccentric loading is around three times of the moment in column under uniform loading
Check for Utilisation Ratios:
The utilisation ratios of the members of MMS under uniform and eccentric loading are provided in the table below:
| Member |
Section Size |
Utilisation Ratio for Uniform Loading |
Utilisation Ratio for Eccentric Loading |
| Column Post |
150CS50x3.15 |
0.7 to 0.8 |
2.0 to 2.2 |
| Rafter |
70CS50x1.5x10 |
0.5 to 0.6 |
1.1 to 1.2 |
| Purlin |
90HU40x25x0.8 |
0.8 to 0.9 |
0.9 to 1.5 |
| Bracing |
60CS50x1.6x10 |
0.5 to 0.7 |
0.3 to 0.5 |
The utilisation ratios of the column posts, rafters and purlins are greater than 1 for eccentric loading, indicating
failure of these members with stresses exceeding the permissible limits. Now, the sections sizes are revised to
maintain the utilisation ratios (stresses) and deflections within the permissible range and similar to that obtained in
uniform loading. The revised section sizes required for eccentric loading are as presented below:
| Member |
Section sizes for Uniform Loading |
Section sizes for Eccentric Loading |
Remarks |
| Column Post |
150CS50x3.15 |
250CS50x3.15 |
Deflections and utilisation ratios observed for both
the types of loading are in the same range and limits.
|
| Rafter |
70CS50x1.5x10 |
100CS40x1.6x10 |
| Purlin |
90HU40x25x0.8 |
90HU40x25x1.0 |
| Bracing |
60CS50x1.6x10 |
60CS50x1.6x10 |
| Tonnage per Table |
456.02kg |
556.96kg |
Thus, the tonnage increment of around 22% is required for the MMS to sustain the eccentric wind loading.
Reference to International Design Standards
A limited research on the International design codes in the direction of application of wind loading on Monopitch canopies clearly validate the application of eccentric wind loading. The references are as provided below:
- American Codes (ASCE 7-16)
Conclusion: SgurrEnergy Recommended Approach
SgurrEnergy has more than 13 years of experience in the design of Module mounting structures for large scale solar PV plants. The Structural Engineering department at SgurrEnergy is involved in continuous research and development for accurate estimation of wind load and studying the behaviour of the mounting structures under such loads.
The Structural design team endorses application of eccentric distribution of wind load as per IS 875(Part 3) for design of the mounting structures and also acquaint the clients about the possible consequences of ignoring the Codal provisions in the design of the structures.
Following upon the case study presented in this technical paper on application of wind loading, SgurrEnergy herein recommends design approach summarised as below:
- The pressure distribution on the modules is not uniform and there is variation in the
pressure applied on the PV modules. This can be attributed to the note no.1 with Table 8
of IS 875 (Part 3):2015 which clearly states that the centre of pressure shall act at 0.3w.
This note is usually ignored by the designers leading to inaccurate design assumptions.
- The variation in pressure distribution on the PV modules validated by the study of the
International design codes indicates that the pressure applied on the entire monopitch
canopy is not same throughout but different based on pressure coefficients.
- The total force coming on the entire assembly / canopy is same in both the cases – uniform
and eccentric loading, only the distribution of force is different on purlins for eccentric
loading. A detailed methodology and sample study to prove the same is provided in the
above chapters.
- Application of eccentric loading on MMS designed for uniform causes the deflections in
column post and rafters to increase by approximately three times as compared to the
deflections obtained for uniform loading. Also, the utilisation ratios (stresses) for the
column posts and rafters get approximately doubled in comparison to the stresses
developed in case of uniform loading.
- The concentration of load on one side of canopy in eccentric wind loading causes increase in the bending moment of column post by around three times. As a result, the deflections and stresses obtained are higher as stated in the point above.
- Based on the above sample study, an increase of around 22% in tonnage may be expected for MMS designed for uniform wind loading to sustain eccentric wind loading.
- The findings and conclusions presented in this article is based on the specific sample input consideration. SgurrEnergy recommends carrying project specific study based on the above mentioned approach.
References:
- IS 875 (Part 3): 2015: - Design Loads (other than Earthquake) for Buildings and Structures
– Code of Practise. Part 3 – Wind Loads Third Revision.
- ASCE 7 -16: - Minimum Design Loads for Buildings and Other Structures.
- EN.1994.1.4.2005: - Eurocode 1: Actions on structures - Part 1-4: General actions - Wind actions [Authority: The European Union Per Regulation 305/2011, Directive 98/34/EC,
Directive 2004/18/EC].
- “Wind Loads on Utility Scale Solar PV Power Plants” by Joseph H. Cain – 2015 SEAOC Convention Proceedings.
- “Wind Load Design of PV Power Plants by Comparison of Design codes and Wind Tunnel Tests.” by O. Bogdan and D. Cretu – Mathematical Modelling in Civil Engineering (Vol.15 – No.3: 13-27-2019).
Download as PDF